为了避免有人没见过树状数组,这里放张图。
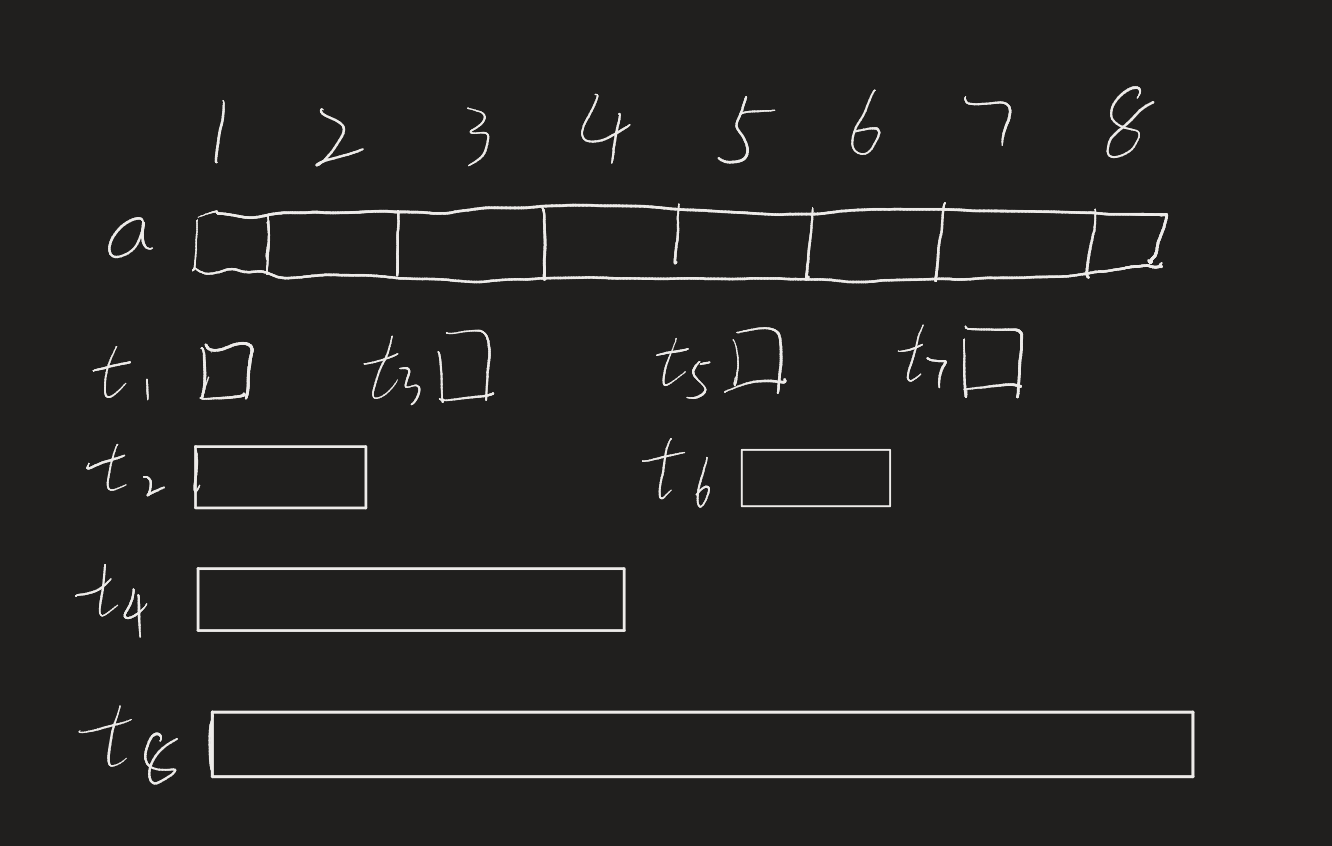
image-20250312154743773图中t数组覆盖的地方就是它的管辖区间,即:
- t[1]=a[1]
- t[2]=a[1]+a[2]
- t[3]=a[3]
- t[4]=a[1]+a[2]+a[3]+a[4]
- t[5]=a[5]
- t[6]=a[5]+a[6]
- t[7]=a[7]
- t[8]=a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]+a[8]
可以看出$t_i$的管辖区间为$[i-\text{lowbit}(i)+1, i]$,其长度为$\text{lowbit}(i)$。
树状数组就是将对原数组的操作转换成对管辖区间的操作,实现了$O(\log n)$的区间操作。
lowbit
这部分就算完全不懂也不影响做题,记住$\text{lowbit}(x)=x&(-x)$即可。
lowbit就是取一个数二进制表示中的最低位的1,比如$\text{lowbit}(6)=\text{lowbit}(0110)2=(0010)2=2$。
还是以$6$为例,算$\text{lowbit}$的全部过程大概是这样:
- 6=(0110)2
- −6=(1010)2
- (0110)2&(1010)2=(0010)2=(2)10
CodeBlock Loading...
单点修改
单点修改时,需要将t数组中所有覆盖这个点的区间都进行修改。
比如,需要修改第$3$个点的值时,t数组需要修改 t[3]、$t[4]$、$t[8]$这三个点。(从$3$那里竖着画一条线,经过的t都需要修改)
怎么找到这条链路呢?可以算一下,其实就是从k开始,下一个点是 k+lowbit(k),一直到n。
CodeBlock Loading...
区间查询可以用类似的方法求得从某个点到n这个区间内所有元素的和。
CodeBlock Loading...
如果要查询 [l,r]区间内元素的和,getSum(r) - getSum(l - 1)即可。
区间修改
这里可以理解为用树状数组维护差分。
先复习一下差分:
- a[1]=d[1]
- a[2]=d[1]+d[2]
- a[3]=d[1]+d[2]+d[3]
- a[4]=d[1]+d[2]+d[3]+d[4]
可以发现: ∑i=1nai=(n+1)∑i=1ndi−∑i=1nidi。
也就是说需要开两个t数组,一个维护$di$,另一个维护$i\times di$。
CodeBlock Loading...
注意此时这两个函数的功能发生了一些变化:
update():从第k位到最后每个元素都 +x。getSum():求第 1位到第k位的和。
